Организм, составленный из уравнений
Сейчас медицина все охотнее и охотнее берет себе в помощь способы из самых различных научных направлений. Так, математика оказывает помощь создать модели той либо другой совокупности людской организма, дабы позже «протестировать» на них лекарственные препараты.
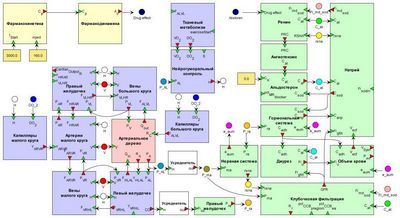
© Илья Киселев
Эксперты из лаборатории биоинформатики Университета вычислительных разработок СО РАН разрабатывают ПО для его организма частей и моделей человека, к примеру, сердечно-сосудистой совокупности. Главный подход тут — модульный: различные блоки, воображающие сердце, венозную или артериальную совокупности и т.д. объединяются в единую структуру подобно громадным программным комплексам.
Для этого эксперты применяют обрисованные в литературе модели, каковые после этого перерабатывают и объединяют. Эти модели заболевания основываются на алгоритмах и уравнениях, выводимых на базе экспериментальных количественных данных.
Универсальных моделей не существует, и ученые обычно придумывают для каждого заболевания собственную, применяя уже устоявшиеся подходы. Они внедряют личные идеи, модифицируют уравнения по экспериментальным данным и в следствии приобретают новую модель.
Подобные структуры вносят значимый вклад в изучение последовательности болезней и смогут оказать помощь совершенствовать способы их лечения.
— Математическая модель каждой системы в организме значительно чаще является набором дифференциальных, реже — алгебраических уравнений, — говорит научный сотрудник ИВТ СО РАН кандидат физико-математических наук Илья Николаевич Киселев. — Значения параметров берутся из уже существующих моделей либо модифицируются для соответствия изюминкам настоящего организма. К примеру, в случае если нужно повысить давление в сосудах (дабы оно было как у гипертоника), возможно расширить значение жесткости их стенок или сделать сосуд более узким, снизив определенный показатель.
Но весьма редко, в то время, когда неясно направление работы, ученым приходится заниматься подбором параметров вручную.
Для этого употребляются методы решения и различные постановки обратных задач. К примеру, задаются замечаемые показатели человека (предположим, давление 140/100 с релаксацией к обычному состоянию), а дальше особые методы находят значения параметров, при которых модель покажет такое же поведение.
Методы разрешают вычислить значения, каковые нельзя узнать конкретно у человека — или абстрактные, или сложно измеряемые: неспециализированное периферическое сопротивление сосудов, их жесткость, ударный и минутный количество сердца. В следствии реально угадать параметры, каковые воздействуют на степень действия лекарства, реакцию организма на физическую нагрузку либо другие условия.
Подобная модель, по сути, догадка о том, как определенные механизмы в организме связаны с замечаемыми параметрами. В случае если модель близка к действительности, она разрешает не только изучить эти механизмы, но и отрегулировать их, «ввести лекарство» и заметить, какие конкретно характеристики в совокупности воздействуют на его эффективность и действие.
— Для валидации математических моделей нами употребляется популяционный подход, в то время, когда моделируется сходу пара организмов, — додаёт Илья Киселев. — Допустим, имеется модель организма с какими-то параметрами: жесткость сосудов, количество желудочка сердца и другие личные главные характеристики человека. Мы создаем множество аналогичных персонифицированных моделей, где любая воображает отдельного человека, а их совокупность есть популяцией, по окончании чего исследуем влияние параметров на чертей популяции в целом.
Это разрешает оценить уровень качества математических моделей на базе данных статистических медицинских наблюдений.
на данный момент ученые ИВТ СО РАН по проекту, поддержанному грантом РФФИ, исследуют действие на «организм» разных препаратов — в частности, «Алискирена» для лечения артериальной гипертонии. Эксперты уже обучились генерировать популяции так, дабы они соответствовали настоящим по таким замечаемым показателям, как давление, количество крови и т.д.
— Мы трудимся совместно с Университетом математики им. С. Л. Соболева СО РАН и НИИ фундаментальной медицины и физиологии, — додаёт Илья Киселев. — Медики предоставляют нам информацию о больных, ИМ СО РАН разрабатывает модели сосудистого русла (сети), а мы объединяем ее с другими моделями — сердца, почки, впредь до отдельных клеток.
Организм описывается в различных масштабах: от целых органов до молекулярного уровня.
на данный момент ученые уже сгенерировали виртуальную популяцию на базе базы данных медицинских обследований и сопоставили модельные и настоящие значения систолического и диастолического давления: как выяснилось, эти показатели прекрасно предсказываются выстроенной учеными из ИВТ СО РАН моделью. Но для пульсового давления таких результатов достигнуть не удалось, что парадоксально, поскольку оно характеризуется отличием между систолитическим и диастолитическим.
— Мы выбрали сердце и кровеносные сосуды, по причине того, что это прекрасно изученная совокупность, для которой делают большое количество моделей, но, не обращая внимания на это, смертность и заболеваемость от сердечно-сосудистых болезней в мире остаётся на первом месте, — заключает ученый. — Так, необходимы новые модели. Важность этого труда в том, что разрабатываемые нами модульные модели сердечно-сосудистой совокупности из нескольких частей смогут открыть новые возможности по персонализации лечебных процессов.
В мире имеется похожие работы, но они показались практически в последние пара лет — на данный момент в математическом моделировании это собственного рода тренд. В любом случае, о программных системах и подобных моделях в Российской Федерации мне не известно.
Источник: Алёна Литвиненко www.sbras.info
c 2.3 Ответ задач посредством уравнений 7 класс 1 часть





















